Investindo no Mercado de Opções

Em Investindo no Mercado de Opções, somos apresentados às ideias fundamentais das opções com uma boa dose de teoria e base matemática.

Este foi o primeiro livro que li sobre opções, apesar de já ter pesquisado sobre o tema antes. Por isso, vou deixar minha impressão como iniciante no assunto, até porque só fiz pequenas operações com opções até o momento.

Nessa obra, Elvis Pfützenreuter propõe entregar conteúdo com uma base matemática mais forte que o que havia disponível na época da publicação. Essa carga teórica pode afastar quem estiver começando, mas certamente será útil para quando o leitor já tiver mais experiência.

Particularmente, eu curti a maior parte dos capítulos, mas devo dizer que as explicações das partes finais já não foram tão agradáveis.

Mas isso será assunto para o final do post. Vamos primeiramente às partes das quais pude tirar o maior proveito.

O que são as opções?

As opções podem soar como algo complexo, mas são mais simples de entender do que parece.

Opção de Compra (Call)

Imagine que você quer comprar ações da empresa XYZ, mas não tem dinheiro suficiente no momento. Então, por uma fração do valor necessário você adquire o direito de comprar aquele papel no futuro por um determinado preço.

O valor que você paga para adquirir uma opção é chamado de prêmio.

Essa data “no futuro”, é chamada data de vencimento. Atualmente, na B3, o vencimento ocorre toda 3ª segunda-feira do mês. A partir de maio de 2021, passará a ser toda 3ª sexta-feira do mês.

Já o preço acordado para a data de vencimento é chamado de strike.

Essa foi a descrição de uma Opção de Compra, ou Call.

Opção de Venda (Put)

Agora suponha que você já tenha ações da empresa ABC e queira proteger a sua carteira de uma eventual queda que esteja por vir. Então, você paga uma certa quantia para ter o direito de vender esses papéis a um preço próximo da cotação atual numa data futura.

Assim, se o preço cair muito, você poderá exercer o direito de vender as ações por aquele preço acordado e conter as perdas.

Essa foi a descrição de uma Opção de Venda, ou Put.

Obrigações de quem vende Call ou Put

Depois que fixamos esses conceitos, podemos pensar no que acontece com quem quer vender — “lançar” seria o termo mais apropriado — as opções.

Se o comprador de Call quiser exercer o direito de comprar as ações em questão, o vendedor de Call terá a obrigação de vender as ações para ele.

Por outro lado, se o comprador de Put quiser exercer o direito de vender as ações, o vendedor de Put terá o dever de comprar esses papéis.

Moneyness

Vamos partir para um exemplo real no homebroker.

Considere que a ação do Itaú (ITUB4) esteja cotada a R$ 24,89 no dia 28/10/2020. A lista a seguir mostra as opções de compra (Calls) disponíveis com vencimento em 18/01/2021.

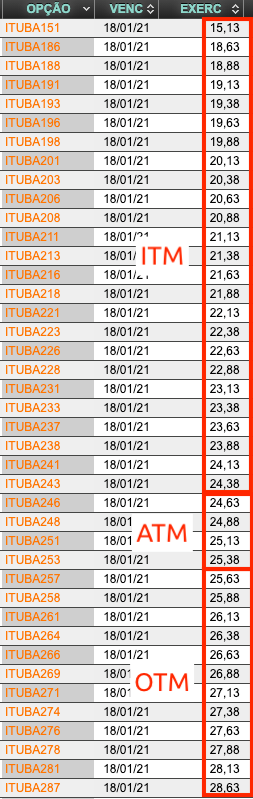
Já vou explicar como entender o código das opções (1ª coluna), que é um pouco mais extenso que o ticker das ações. Mas antes, quero falar de algo chamado moneyness.

Se comprarmos alguma dessas opções da imagem, só fará sentido exercê-la se ela tiver um preço de strike (coluna “EXERC” da tabela) menor que a cotação da ação no momento do exercício.

Lembrando que há basicamente duas modalidades de opções: as americanas, que podem ser exercidas a qualquer momento até o vencimento, e as europeias, que só podem ser exercidas no vencimento.

Ao exercermos esse direito de compra, adquirimos a ação a um preço mais barato que o negociado no mercado e poderemos vendê-la com lucro em seguida.

Nesse caso, dizemos que são opções “dentro do dinheiro” ou in the money (ITM).

Quando são opções com o strike próximo da cotação, dizemos que estão “no dinheiro” ou at the money (ATM).

E quando o strike estiver muito distante, para o lado em que não será interessante exercer a opção, dizemos que ela está “fora do dinheiro” ou on the money (OTM).

Fazendo as devidas adaptações, os mesmos termos valem para opções de venda.

Código das opções

Agora sim, vamos entender o código das opções.

As primeiras letras se referem ao ticker da ação em questão. No caso do nosso exemplo, ITUB.

A letra seguinte informa ao mesmo tempo se é uma Call ou Put e em qual mês é o seu vencimento. As Calls vão de A a L (A: janeiro, B: fevereiro, C: março, D: abril e assim sucessivamente) e as Puts de M a X. No nosso exemplo, vemos ITUBA porque o vencimento é em janeiro.

Já o número no final é uma indicação aproximada do preço de strike, como em ITUBA251 que tem o strike em R$ 25,13.

Mas atenção: confira sempre o strike porque o código eventualmente indica um preço que não combina precisamente com o strike (após a distribuição de dividendos, por exemplo, ocorre um ajuste no strike).

Muito bem! Acho que esse é o mínimo que se precisa saber para entender a utilidade das opções.

É claro que há muitos outros conceitos fundamentais, como valor intrínseco, valor extrínseco, margem etc., mas vamos avançar que quero compartilhar outras ideias interessantes.

Capital Asset Pricing Model (CAPM)

O CAPM é um modelo — uma equação matemática — que busca estimar a relação entre risco e retorno de um ativo, especialmente ações.

Abaixo está a fórmula e em seguida explico cada um dos termos:

$$ r_{a} = r_{f} + \beta_{a} . (r_{m} - r_{f}) $$

$$ r_{a} $$

$$ r_{f} $$

$$ \beta_{a} $$

$$ r_{m} $$

$$ (r_{m} - r_{f}) $$

Pegando novamente o Itaú como exemplo, vamos começar consultando o beta de ITUB4 segundo o Yahoo Finance. Atualmente o site mostra 1,05.

A taxa de retorno livre de risco será a SELIC atual, que está em 2% ao ano.

E o retorno médio do mercado será a média do retorno anual do IBOV nos últimos 10 anos, que foi de +5,96% ao ano.
2010: +1,79%
2011: -5,26%
2012: -5,25%
2013: -20,28%
2014: -1,53%
2015: -13,86%
2016: +60,05%
2017: +31,30%
2018: +14,70%
2019: +2,08%
Média: +5,96%

Aplicando os valores acima na fórmula do CAPM, temos:

$$ r_{(ITUB4)} = 2\% + 1,05 (5,96\% - 2\%) $$

$$ r_{(ITUB4)} = 0,02 + 1,05(0,0396) $$

$$ r_{(ITUB4)} = 0,02 + 0,04158 $$

$$ r_{(ITUB4)} = 0,06158 = 6,16\% $$

Certo, mas o que esse número significa?

Ele quer dizer que quem investe em ITUB4 espera que a ação dê 6,16% de retorno ao ano, de modo a compensar o risco envolvido nessa escolha de investimento.

Agora, para fazermos uma comparação, vamos ver como ficaria o cálculo para uma ação com beta menor que 1.

Pegaremos ENBR3, que no momento tem beta igual a 0,29.

$$ r_{(ENBR3)} = 0,02 + 0,29 (0,0396) = 0,02 + 0,011484 = 0,031484 = 3,15\% $$

Como ENBR3 tem um beta menor que o de ITUB4, naturalmente o seu retorno esperado será inferior. Nesse caso, foi de 3,15%.

Vale destacar que:

• o retorno esperado calculado via CAPM NÃO determina que o ativo terá aquela rentabilidade;
• ações de maior risco NÃO necessariamente oferecerão um retorno maior.

Estamos falando de uma avaliação. Um modelo é uma aproximação da realidade, e nem sempre ele é capaz de prevê-la.

Modelo Black e Scholes

Na resenha do livro A Fórmula Mágica de Joel Greenblatt para Bater o Mercado de Ações, vimos uma forma simples de fazer o valuation de uma empresa.

A partir de modelos mais sofisticados, analistas avaliam quanto vale uma companhia, e com isso são capazes de calcular se suas ações estão sendo negociadas a um preço justo ou não.

Mas será que para as opções também conseguimos estimar qual é o preço (prêmio) adequado?

Sim! E uma das formas mais conhecidas é o modelo criado por Fischer Black e Myron Scholes, e aperfeiçoado por Robert Merton, conhecido como modelo Black-Scholes.

Ele rendeu a Scholes e Merton o Nobel de Economia em 1997. Black certamente compartilharia do prêmio, mas infelizmente veio a falecer dois anos antes.

Dito isso, você já deve estar esperando cálculos complicadíssimos. De fato, são algumas fórmulas nada triviais, mas a boa notícia é que você encontra sites que calculam isso facilmente.

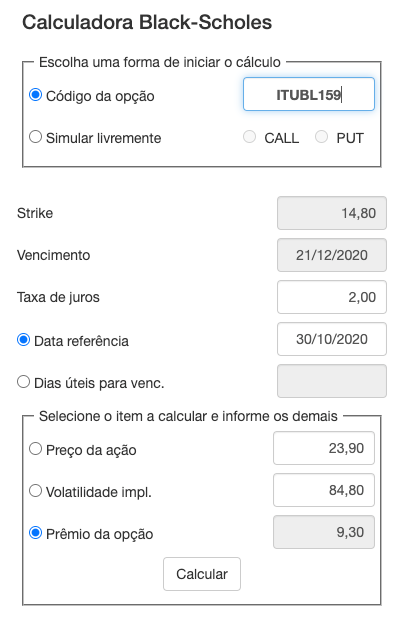
Com a calculadora Black-Scholes do Opções.net.br, por exemplo, conseguimos calcular o prêmio esperado de uma opção apenas inserindo o seu código de negociação e a taxa de juros atual. Os outros parâmetros são preenchidos automaticamente.

Lembrando que esse modelo é indicado para opções europeias, aquelas que só podem ser exercidas no vencimento.

Para finalizar, quero dizer que fiquei um pouco confuso com as explicações sobre operações com opções (trava de baixa, trava de alta, vaca etc.). O autor oferece as características gerais em uma tabela e em seguida mostra gráficos, probabilidades e cenários possíveis.

Talvez pelo menos nesses capítulos poderia ter aliviado na parte teórica.

Outro ponto importante de comentar é que a edição do livro é de 2008, o que pode incomodar alguns leitores.

Mas, pelo que pude verificar, o autor tem um livro mais recente, de 2018, com mais prática do que teoria — o Ganhando Dinheiro com Opções. A conferir.

Enfim, no geral eu acredito que a obra tem mais pontos positivos do que negativos. É mais indicado para quem quer estudar os aspectos técnicos das opções e provavelmente não é a melhor opção (com o perdão do trocadilho) para quem procura um 1º livro sobre o tema.

ATUALIZAÇÃO: até a publicação deste post, este livro estava na 1ª edição. Em 2021 foi lançada a 2ª edição da obra.